プロクラシスト

今日の寄り道 明日の近道

【注目記事】 Pythonでゼロから機械学習/データ分析を学ぶためのサイトマップ

【2017年東大数学】『酔っぱらいの動き方』を計算する＋α

理系ネタを全力で

スポンサーリンク

こんにちは、ほけきよです！ 先週、国立の合格発表が終わりましたね。

合格された方、おめでとうございます。春から人生の夏休み、楽しんでください。 不合格だった方、たったの1回くらいで人生は決まりません。夢や目標を持っているならば、持ち続けてがんばってください。

私も塾講師業界に数年いたものですから、未だに入試問題が気になります。

高校、大学生の頃は紙とペンでうんうん解いていたのですが、 最近は高校生の頃と違ってプログラミングという便利なものもを覚えましたので、 今日は東大入試の問題をコンピウタの力を借りて解いてみようと思います！

解く問題：東大理系数学第2問『酔っ払いの動き』

f:id:imslotter:20170314201415p:plain

パット見た瞬間「あ、ランダムウォークだ！！」 となりますね。東大の問題にしては簡単ですなぁ。 *1

まあいいや、その辺に模範解答的なのは載っていると思うので、 私はゴリ押しで解きますね。

ランダムウォークとは

日本語では『酔歩』ともいいます。いわゆる「酔っぱらいの千鳥歩き」みたいなもんですね。

右も左も分からない酔っぱらいが、夜中にほっぽりだされたら、どんな風になるのか。 これ、実は数学的に、そして物理的に、そして経済などにもつながる深い、深い学問なんです。

あとでちょっとだけ話します^^

実装して解く

こういう何回も試行を繰り返しながら進んでいくような計算、コンピウタは得意ですよね。ボクはそう習いました。

  • 乱数を用意する
  • 1/4ごとに上下左右座標(m,n)を移動する
  • 6回繰り返したとき、(1)m=n ならTrue (2) m=n=0ならTrue
  • この一連の流れを1セットとし、収束するくらいセット(今回は1000000セット)を繰り返す。
  • 1000000セット中何回(1), (2)のTrueが出たかを数える

以上です。本来なら分散値とか調べて有意水準～～とかするところなんですが、 めんどくさいので適当にアタリをつけながらやっちゃいましょう。

ちなみにランダムウォークの様子はこんな感じです。酔っ払いが歩いている感じですね^^

f:id:imslotter:20170315215604g:plain

6秒後に緑の点線に乗るかどうかが問(1), 赤の点に行くかが問(2)です。

結果

1000000セット試行した結果の(1)と(2)の確率はこちら。 左が(1)の結果、右が(2)の結果です。

(0.313045, 0.097846)

しかし、これじゃ多分正解にはならないんですよね。 東大の回答が求めているのは分数ですし。 なので、分数になりそうな数を探しましょう。

一回の試行が{\frac{1}{4}}ずつ確率を掛けていくので{\frac{M}{4^{N}}} みたいな形になっているはずです。

さっきの結果に{4^{N}}ずつ掛けていった結果がこちら

4**1 : (1.25218, 0.391384)
4**2 : (5.00872, 1.565536)
4**3 : (20.03488, 6.262144)
4**4 : (80.13952, 25.048576)
4**5 : (320.55808, 100.194304)

はい！！それっぽい数が出てきましたね。 答えは

  • (1) {\frac{5}{16}}
  • (2) {\frac{25}{256}}

です✌︎(‘ω'✌︎ )　あってたーーー！

t=6秒以上ランダムウォークさせるとどうなるの？

t秒後に元の位置にいる確率は？

これだけじゃ味気がないし、せっかくコンピウタに解かせたので、もうちょっと色々やってみます！！

まずは、tを無限大にすると、(1), (2)の確率ってどうなっていくのか、調べてみました。結果はこちら

f:id:imslotter:20170315220215p:plain

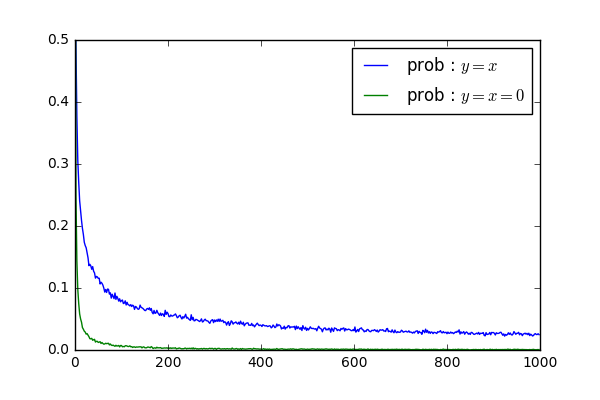
どんどん0に近づいていきますね。酔っ払いを放置し続けていくと、戻れなくなるということがわかりますね。 ちなみに余談ですが、(2)の確率 = (1)の確率2 が成り立つようです。なぜかは考えてみてください*2

一度も元に戻れない確率(再帰性)

tを大きくすると、 t秒後には元の位置に戻っている可能性が低くなっていくことはわかりました。割と直感的だと思います。 では、次の問いならどうでしょうか。

酔っ払いがずっと歩いていて、一度も元の位置に戻らない確率

さっきと違うところは、t秒後とかじゃなくて、どこかのタイミングで戻れたらいいのです。 つまり、ずっと待っていて、元の位置に帰ってきた瞬間、誰かがその酔っ払いを確保できれば成功！というイメージです。

少し難しいので、結論だけ話すと100%帰ってこれることが数学的に保証されています。酔っ払いだったとしても、無限時間待っておくと必ずお家に帰ってきます！安心してください！

これをランダムウォークの再帰性と言います。興味のある人は、ググってみてください！

面白いのが、3次元ランダムウォークになると、100%戻ってくる保証がなくなるところです。動きに自由度がありすぎて、1度も元に帰って来ないまま、行方不明になっちゃうんですね。帰って来れるのは2次元までです。

t秒後にどのくらいまで動くの？

tが大きくなると、元に戻れる確率がめちゃくちゃ低くなるということは、t秒後には酔っ払いは原点から遠く離れているということが予想できます。

そこで、次の問いです

t秒後、酔っ払いは大体どのくらいまで進んでいるのか

これも、最終位置との距離を算出すれば簡単に出せます。結果はこちら

f:id:imslotter:20170315224817p:plain

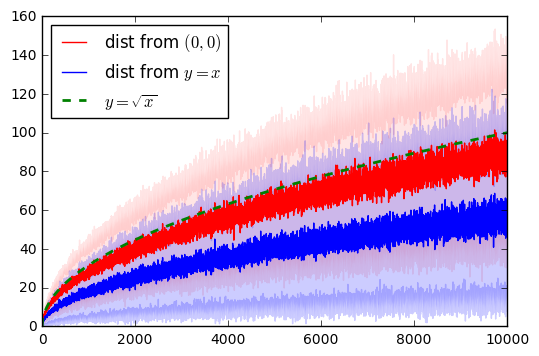
赤の線が原点からの距離、青が{y=x}からの距離です。薄いのは標準偏差です。 比較用に{y=\sqrt{x}}も載せてみました。どうやら距離の平方根と関係がありそうというのがわかりますね。

結論としては

「酔っ払いはT秒歩くと大体元の位置から{\sqrt{T}}の位置にいる」

ということです。

これも数学的に、原点からの距離は時間の平方根に比例することが知られています。*3 この関係は、アインシュタインの関係式と呼ばれて、物理や金融での不確実性を含んだ現象を説明するのにほぼ必須の、非常に重要な関係式となっています。 ここから、例えば熱がどういう風に伝わっていくか*4とか、金融商品の価格を決める方程式*5とか、世界が広がっていくんです。楽しいですね〜〜！

赤と青の線の関係は？

さあ、最後です。さっきの図で、酔っ払いの進む距離は進んだ時間の平方根に比例することがわかりました。それが赤色の線です。でもみてみてください。青色の方も平方根に比例してそうですよね。赤と青には何らかの関係性がありそうです！

ということで、横軸に原点からの距離、縦軸に{y=x}からの距離をとってみて、その関係性を可視化してみます。

f:id:imslotter:20170315232905p:plain

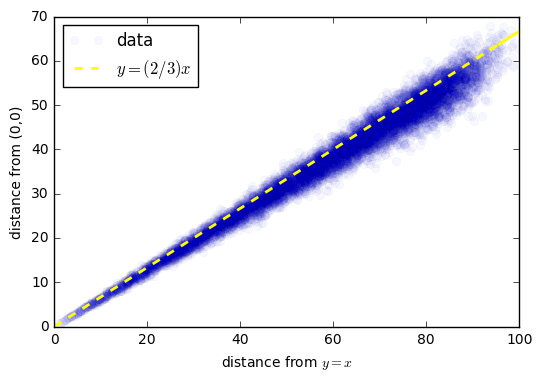
綺麗な比例の関係が出てきました！ それで何となく、1.5倍くらいかな？と思ったので、それらしき線(黄色)を引いてみました。割と合ってそうですよね。

傾きはどこからきたの？

でも、点を集めて比例になったからって、その傾きが2/3であるという数字の根拠はどこにもありませんよね。この比例の傾きはどこからきたのか、少し考察します。

この時、私は何となく直感的に、{\pi}が傾きに含まれてくれれば嬉しいなぁ。と思ったんです。なぜか。 この問題、円と関わりがあるなと思ったからです。

酔っ払いが進む距離はさっきまでの話で見積もれましたが、どの方向に進むかまでは全く見積もれてませんよね。 そう、完全ランダムに方向は決まるのです。めちゃくちゃ大雑把に図を書くと,　t秒後には大体半径{\sqrt{t}}の円周上にいるだろうということになります。

f:id:imslotter:20170315233903p:plain

じゃあ、そこから{y=x}の距離ってどのくらいなんでしょうか。次の図をご覧ください。

f:id:imslotter:20170315234554p:plain

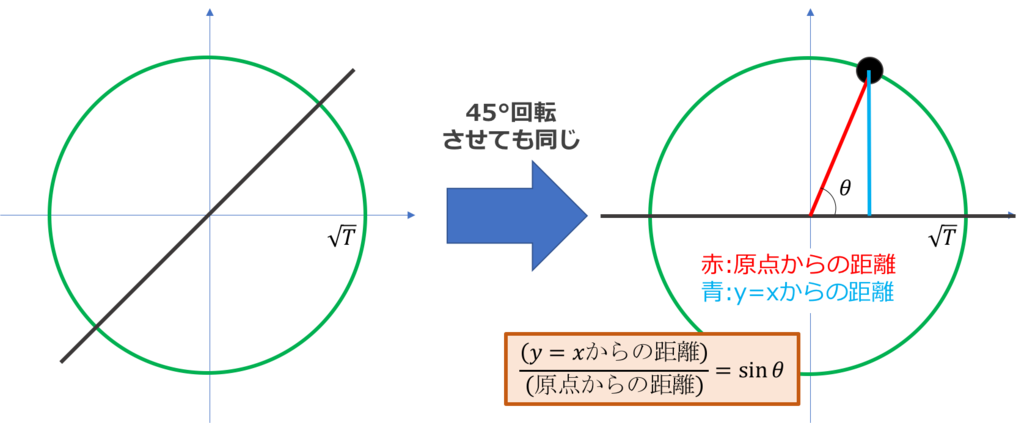
図のように角度{\theta}で表されることがわかりました。 さて、さっきも言ったように、酔っ払いの方向は完全にランダムのはずなので、大体円周上に等確率に位置しているだろうということがわかります。

よって距離の比の期待値が、角度の積分で次のように計算することができます。

f:id:imslotter:20170316005508p:plain

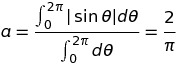
はい、出てきました！{2/\pi}!! これをさっきのグラフの上にはめてみると

f:id:imslotter:20170316002844p:plain

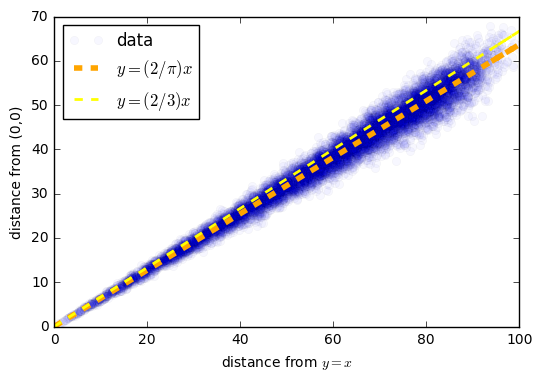
ぴったり合うことがわかります。こういうとき、一番うれしい＼(^o^)／笑

終わりに コンピュータにできること、人がしなければならないこと

入試問題としては簡単な問題でしたが、いろいろと応用の幅が広く、また学問的にも重要な問題でした。 最後に取り上げたいのは、コンピュータで出来ることと出来ないことです。

今回

  • 大雑把に確率を算出する
  • どんな関係式があるかをプロットして関係を探る

はコンピュータにさせました。実験が一瞬でできるの、最高ですね。いろいろな発見があって面白かったです。ただし、全てをコンピュータでやったわけではありません。

  • 分母が4Nであろうという推論
  • 一般化する(時間を無限大にまでする)という発想
  • 背後に隠された法則を考える思考

これらは人の頭を使ってやったことです。そして、まだまだコンピュータには出来ないことだろうと思っています。

とはいえ、このような複雑系科学だったり、実世界に近いところで行う学問は、どうしてもデータの力を借りなければなりません。 私は、『コンピュータはあくまで人が法則を発見するための補助ツール』だと思っています。 人間はコンピュータが頑張って出してくれた実験結果に対し考え、新発見をしていかなければなりません。

いろいろな事実から普遍の法則を発見する。 それがコンピュータと人間の差であり、また、学問をしていて一番楽しい瞬間の一つなのでしょう。 今回の係数{\frac{2}{\pi}}の発見は、既知の事実かもしれませんが、私の中ではとっても嬉しい発見でした。

まだまだコンピウタには負けません！けどコンピウタには色々と助けてほしいです。特異点など起きず、仲良く暮らしていければいいですね。 ではではっ！

コード(python)

とりあえず、ランダムウォークする部分と、そこから確率を算出する部分だけ載せておきます！ 適当に改変しながら使えると思うので、適当に実験してみてください。

import numpy as np

class RandWalk:
    def __init__(self):
        self.m = 0
        self.n = 0
    
    def move(self):
        rnd = np.random.random()
        if rnd <= 0.25:
            self.m += 1 # x方向に+1
        elif 0.25 < rnd <= 0.5:
            self.n += 1 # y方向に+1
        elif 0.5 < rnd <= 0.75:
            self.m -= 1 # x方向に+1
        elif 0.75 < rnd:
            self.n -= 1 # y方向に-1
   
    def question1(self):
        if self.m == self.n:
            return 1
        else:
            return 0
        
    def question2(self):
        if self.m ==0 and self.n == 0:
            return 1
        else:
            return 0

def experiment(N, iteration):
    """
    N : ランダムウォークを続ける秒数
    iteration : 実験の回数
    """
    count1,count2 = 0, 0
    for i in range(iteration):
        RD = RandWalk() #初期化
        for i in range(N):
            RD.move()
        count1 += RD.question1()
        count2 += RD.question2()
    return count1*1.0/iteration, count2*1.0/iteration

prob1, prob2 = experiment(6,1000000)
print(prob1,prob2)

*1:東大の名誉のために言っておきますが、秒数を6にしたのは絶妙だと思います。だって、解けそうだから。 こういう時のセオリーは実際の値に惑わされず一般化ですぞ！受験生諸君、覚えておくように！

*2:どこかの模範解答に載るっていた気がします。

*3:期待値と分散の計算を行うと、そうなります。

*4:拡散方程式

*5:ブラックショールズ方程式

imslotter

関連記事
スポンサーリンク


PROCRASIST をフォローする
コメントを書く

PROCRASIST