素数ファンの皆様こんにちは、ほけきよです。
2017年が始まって二週間が経過しようとしてますね! 2017年といえば、そう、素数ですね!素数ファンならすぐにお気づきになると思います!!西暦0年から306回目!
この前の素数が2011年だったので、実に6年ぶりの素数年というわけです。 この、2011年は連続する11個の素数の和であるということで、世界中が沸いていたと思います。 (2011 = 157 + 163 + 167 + 173 + 179 + 181 + 191 + 193 + 197 + 199 + 211)
「じゃあ、2017年は他に面白いことないの??」
お任せください!それでは、2017に関するエトセトラ、紹介していきます!
セクシー素数
セクシー素数とは差が 6 の素数の組 (p, p + 6)のことです 2011年が素数だったので、(2011,2011+6)でセクシー素数というわけです!
なおこの用語は、ラテン語で 6 が sex であることに由来するものであり、性的な意味のセクシーとは無関係である。(Wikipediaより)
ピタゴラス数
もしかしたらピタゴラス数なのでは?? なんて思いながら、ちょっとプログラムを組んで調べてみました。*1 ちなみに、if文の中身を変えるといろいろと応用できるかもしれません。あなただけの2017を見つけてみてください^^
#coding:utf-8 import sympy # 素数のピタゴラス数を調べる def pita(N): A = range(N) if sympy.divisor_count(i)!=2: return False for a in A: for b in A[a:N]: if N**2 == a**2+b**2: print("{}^2+{}^2={}^2".format(a,b,N)) #素数のピタゴラス数を見つける for i in range(2017): # 素数かつピタゴラス数 pita(i) >>> ... >>> 315^2+1972^2=1997^2 >>> 792^2+1855^2=2017^2
本当にピタゴラス数だった!その前が
というわけで、実に20年ぶりの素数のピタゴラス数ということになります。
図形で表すとこんな感じです、2017年三角形、使っていきましょう!

ピタゴラス素数
ピタゴラス数を見つけたので、
と思っていたのですが、実は、ピタゴラス素数は別の定義を指すようです。 それがこちら
これについても、調べてみると、ありました!
また、これに関しても
実を言うと、ピタゴラス素数は、必ずピタゴラス数の組を持つのです。証明はこう
が存在するとすると、両辺を2乗して、
式変形をすると、
つまり、
が、ピタゴラス数の組(終)
図形にすると、こう

3つの立方数の和
は存在しない。
ですね。でも、これが
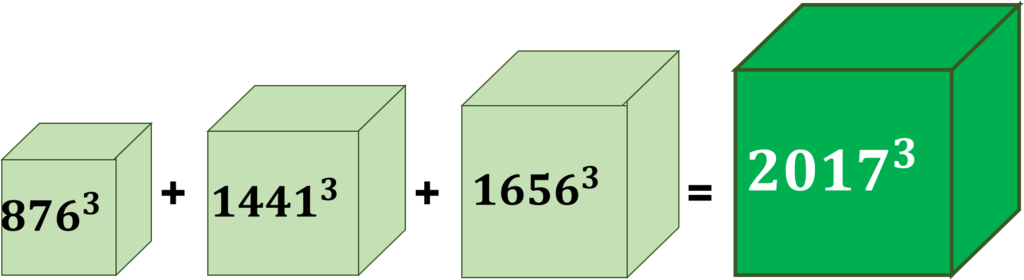
になると意外と結構存在するんです。2017は
と、2組ありました!ちなみにその前は1999年で、
なので、18年振りですね!
図的に表すとこんな感じです!
数検の2017年問題
数検の問題でこんなのがあったので、解いてみました

- 解答
に
を代入すると
ここから、ある整数を取り除いて2017にするのだから、
したがって、
つまり、以下の等式が成り立つわけです!
分だけ足りないのですね、惜しい!後8年待ちましょう^^
整数の辺だけを持つ正七角形の一辺
いろいろと遊んでいたんですが、もっともっと高度な遊びをしている方、やはりいらっしゃるんですね。
7 で割って 1 あまる素数 でもある 2017 は, (とある条件を満たす)整数の辺だけを持つ7角形の一辺
虚数方向に素因数分解をするとは…*2発想がやばい。(褒め言葉:最上級) その図形がこちらです!2017図形!!
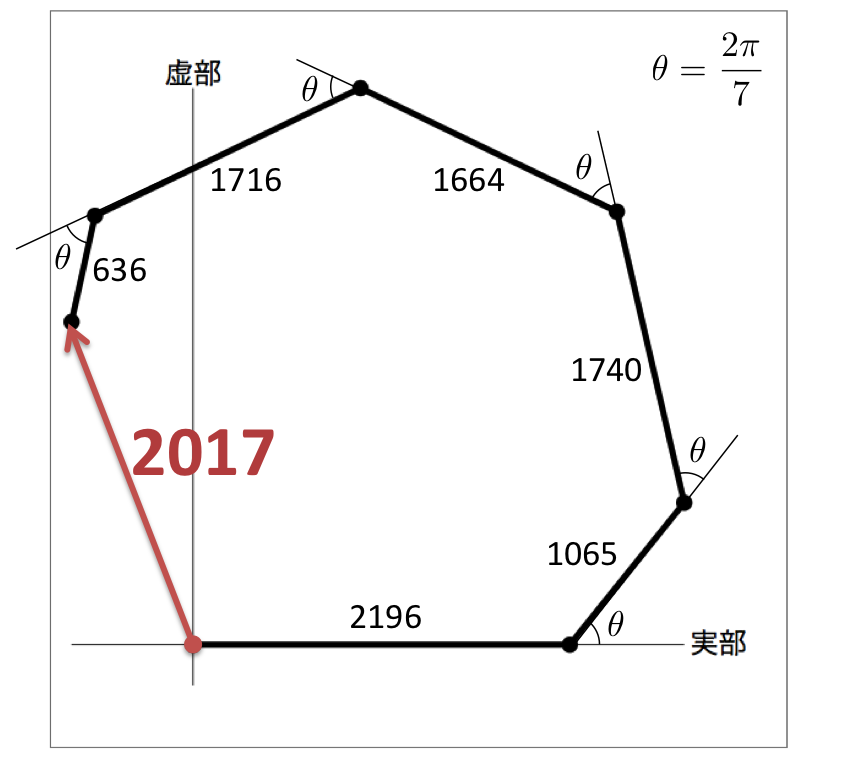
id:tsujimotterさんの苦労話を読んだ*3後にこの図形を眺めると、非常に味わい深いですね。すごい人はいるものだ。
ちなみに7で割って1余る次の素数は2087年なので、みなさんこの7角形を大事にしましょうね!
随時更新します
2017年、他にもいろいろと見つけたり思いついたりすれば追記していこうと思います。 ではでは!
