機械学習で使う指標総まとめ(教師あり学習編)

こんにちは、ほけきよです！

機械学習の基本は教師あり学習です。でも、実際の現場ではいろいろ指標が出てきて「?」ってなるので、一回本気でまとめてみることにしてみました！

教師あり学習の分類
二値分類
多クラス分類
出力が数値(回帰)
時系列問題
参考になりそうなサイト

教師あり学習の分類

今回は正解はカテゴリか意味を持つ数字かで場合分けをしてみた。全体の指標のサマリーはこんな感じ(だと思っている。)

f:id:imslotter:20170517111553p:plain

※他にも大事な指標があるよ&これは間違っているのでは？？というコメントは絶賛受付中なので、教えてください。

二値分類

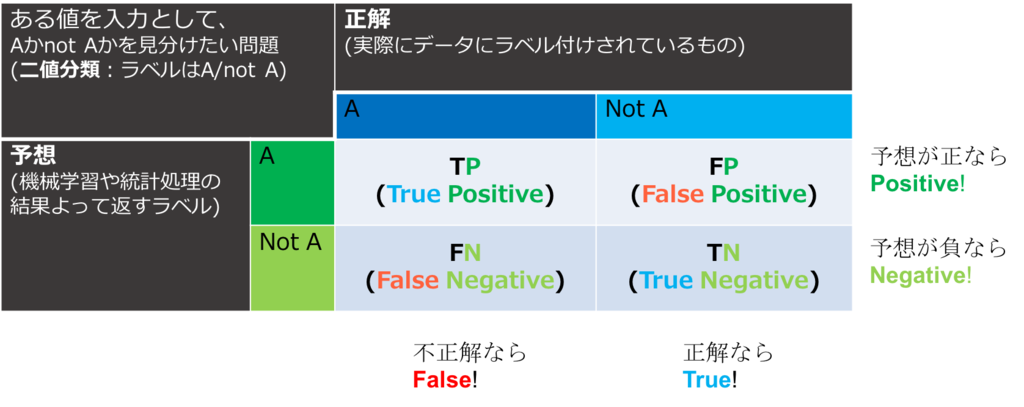
Aである or Aではないを分類

用語一覧表

用語	日本語	定義・意味
Confusion Matrix	混同行列	データを上手く分類できたかどうかを表す表。ここでは、列方向は正解、行方向は予測
True Positive (TP)	真陽性	正しいと予測して正しい
False Positive (FP)	偽陽性	正しいと予測して正しくない
True Negative (TN)	真陰性	正しくないと予測して正しくない
False Negative(FN)	偽陰性	正しくないと予測して正しい
Accuracy	全体正解率	予測に対して答えがどのくらいあってたか ${Accuracy = \frac{TP+TN}{TP+FP+TN+FN}}$
Precision (TPR)	適合率	正しいと予測したものうち、本当に正しいのは？偽陽性を低く抑えたい時に見る。病気じゃないと予測して病気だった場合とか困る。 $Precision=\frac{TP}{TP+FP}$
Recall	再現率	見つけるべきもののうち、正しく見つけることができたものの割合。Sensitivity(敏感度)ともいう。偽陰性を低く抑えたい時に見る。 $Recall = \frac{TP}{TP+FN}$
False Positive Rate	偽陽性率	実際に正しくないもののうち、何%間違ったか。 $FPR = 1-Specificity = 1-\frac{TN}{FP+TN}=\frac{FP}{FP+TN}$
F-measure	F値	適合率と再現率のトレードオフに対してそのバランスを見る値。 $\frac{1}{F-measure}=\frac{1}{2}\left( \frac{1}{Recall}+\frac{1}{Precision} \right)$
Weighted F-measure	重み付きF値	目的に応じて、PrecisionかRecallのどちらかを重視するなどを決めることも可能 $\frac{1}{F-measure}=\frac{1}{1+\beta^{2}} \frac{1}{Recall}+\frac{\beta^{2}}{1+\beta^{2}}\frac{1}{Precision}$ $\beta=1$ でF値, $0 \lt \beta\lt 1$ でRecall重視, $1 \lt \beta$ でPrecsision重視
Precision-Recall Curve	*	横軸Recall, 縦軸Precisionでプロットしたもの。トレードオフの関係なので、単調減少なら良い。
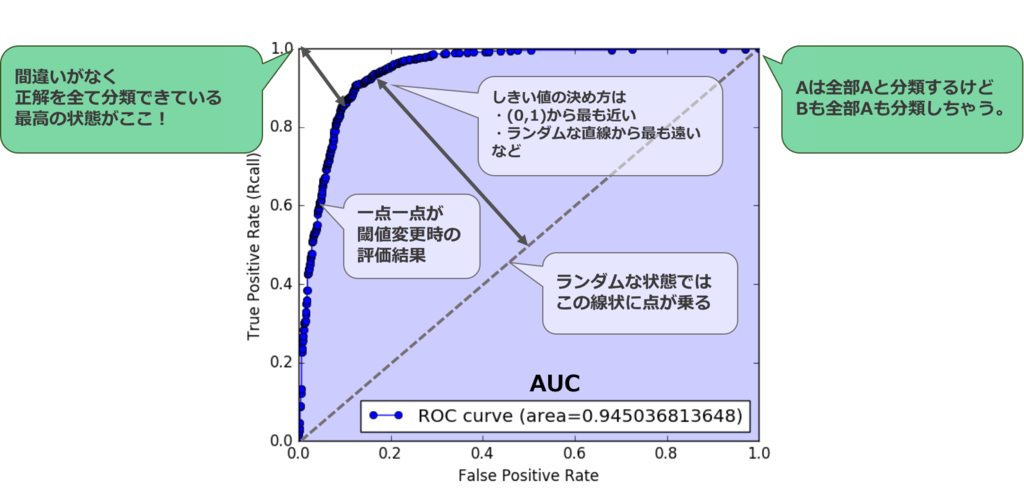
ROC curve	受信者動作特性	横軸が偽陽性率, 縦軸が敏感度でプロットしたもの。(真陽性と偽陽性の関係性を示している)普通偽陽性が上がると真陽性も上がる(なんでも正しい！と言っときゃいい)ので、偽陽性が低い時に真陽性が1に近づくのが理想
AUC	ROC曲線下面積	ROC曲線の積分値。理想は1
Logarithmic Loss	対数損失	確率で出力が出る時(ソフトマックス関数)などをそのまま評価する方式。

図解

f:id:imslotter:20170517094644p:plain

事例

事例1:果物の分類

	みかん	みかんじゃない
みかん	45	10
みかんじゃない	5	40
計	50	50

Acuraccy = (45+40)/(50+50) = 0.85
Precision = 45/55 = 0.82
Recall = 45/50 = 0.90
FPR = 1- 40/50 = 0.20
F-measure = (2×0.9×0.82)/(0.9+0.82)=0.85

こういう場合は、正しく分類できているかどうかが大事なので、Accuracyを見るのが良さそう。

事例2:ガンかどうかの検査

	ガン	ガンじゃない
ガン	8	90
ガンじゃない	2	900
計	10	990

Accuracy = (8+900)/(10+990) = 0.908
Precision = 8/(8+90) = 0.082
Recall = 8/(8+2) = 0.80
FPR = 1-90/990 = 0.91
F-measure = (2×0.8×0.082)/(0.8+0.082) = 0.148

こういうh場合、Precision（正解と判断したものが本当に正解か）は正直どうでもいい。精密検査をすればいいだけ。それよりもRecallが1より小さい方がまずい。ガンじゃないと判断して、ガンだったら訴訟モノなので、是が非でもここを1に持っていきたい。

ROC曲線の意味合い

ROC曲線で大事なポイントを一枚絵にしてみた。 f:id:imslotter:20170517120406p:plain

指標まとめ

特定の閾値を設定せずに評価したい場合 -> ROC, AUC
特定の閾値を設定して評価したい場合
- Aである、Aでないの重要度が一緒の場合 Accuracy
- Aであると言う事実が重要な場合
  - Aであると予測して、実際にAであった人の割合が重要(試験、再検査にコストがかかるなど)な場合 -> Precision
  - 実際にAである人をきちんとAと予測できているか(Recall)が重要(検知漏れが許されない) -> Recall
  - 両方を見たい場合 -> (weighted) F-measure

多クラス分類

使う指標はだいたい二値の時と同じだが、overallとaverage, microとmacroという概念が出てくる*1

	みかん	りんご	ぶどう
みかん	91	1	3
りんご	5	17	1
ぶどう	4	2	1
計	100	20	5

precision, recall, F-measure

参考 : Quara “What are some good error metrics for multi-class classification?”

SVMとかの分類面を一本引くというようなやつは、それぞれのクラスについて、クラスかそうじゃないかを分類していく(one versus othersもしくはone versus one)ので、それぞれのクラスにおいて表ができる。このような時の評価には、precisionやrecall、F-measureを使って評価することが良い。

micro precision : 一つのセル単位に着目
$\frac{TP(orange)+TP(apple)+TP(grape)}{TP(orange)+TP(apple)+TP(grape)+FP(orange)+FP(apple)+FP(grape)}$
macro precision : 一つの表単位に着目
$\frac{1}{3}\left(\frac{TP(orange)}{TP(orange)+FP(orange)}+\frac{TP(apple)}{TP(apple)+FP(apple)}+\frac{TP(grape)}{TP(grape)+FP(grape)}\right)$

他のrecallも同じ。

F-measureについては、micro/macroで出てきたprecisionとrecallの調和平均を取ればOK

acurracyも、イメージとしてはoverallがmicro, averageがmacroと捉えることができる。

計算するとこの通り

	micro	macro
Precision	0.856	0.613
Recall	0.856	0.653
F-measure	0.856	0.632

microは全体のデータ数を考慮する
macroは各クラスごとの影響はデータ数に関係なく等しいとしている。

見たいものが何であるかによって使い分ける

accuracy

one-versus-anotherではなくて、入力するとどのクラスかを当ててくれるような分類器(ニューラルネットなど)だと、ひとまとめの表で、次のようなConfusion Matrixを書くこともできる

f:id:imslotter:20170517111850p:plain

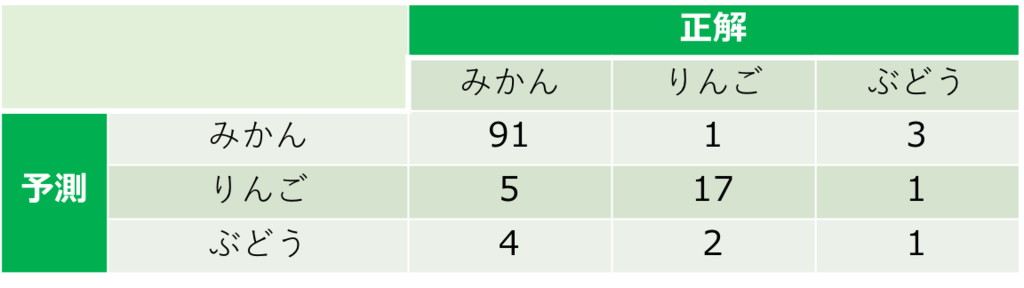
accuracyは、overall accuracyと、average accuracyがある

用語	定義・意味
overall accuracy	全体の精度
average accuracy	各クラスのaccuracyの平均。クラスを平等に扱う

上の事例を使うと、

$overall\,accuracy = \frac{91+15+1}{100+20+5} = 0.856$
$average\,accuracy = \frac{1}{3}\left(\frac{91}{100}+\frac{17}{20}+\frac{1}{5}\right) = 0.653$

average accuracyは小さな数の正確さも同等に評価するようになる。

logarithm loss

ニューラルネットとかは、予測モデルの出力が、そのクラスに属する確率で記述されることが多い(ディープラーニングで、出力層がクロスエントロピーの場合とか)。

そこで、Logarithm Lossという指標を用いることがよくある

f:id:imslotter:20170517103904p:plain

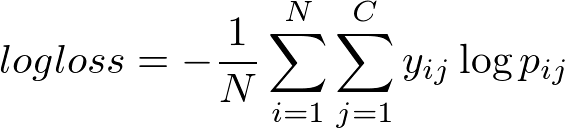
$N$ : データの数
$C$ : クラスの数
$p_{ij}$ : i番目のデータが、クラスjに属する確率
$y_{ij}$ : i番目のデータがクラスjに属するか否か(属していれば1, 属してなければ0)

$p_{ij}$ はいわゆる分類器の自信のようなもので、これが高いほど自信を持って答えられていることになるので、lossは小さい、となる。このように、分類の結果だけを見るのではなく、分類に至った過程まで見るのがlogarithm loss

出力が数値(回帰)

カテゴリの1,2,…には意味はない。ここは意味を持つ値を予測したいときに評価するもの。

用語一覧

${y_i}$ : 正解
${y_{est}}$ : 予想の値
$\bar{y}$ : 平均

用語	日本語	定義、意味
Mean Squared Error	平均二乗誤差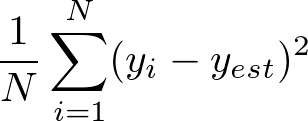
Root Mean Squared Error RMSE	平均二乗平方根誤差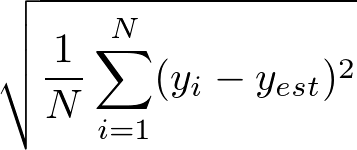
Mean Absolute Error	平均絶対誤差
Coefficient of Determination	決定係数	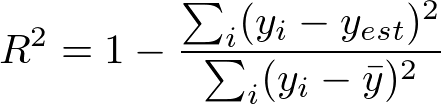回帰直線の当てはまり具合を示すもの。平均からのばらつきが分母にあり、相対値として与えられる。
AIC	赤池情報基準	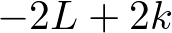Lは尤度。kはパラメータの数。複雑なモデルは過学習を引き起こすので、その罰則というイメージ
BIC	ベイズ情報基準	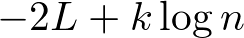nはデータの数
wAIC	(渡辺？)AIC	AICをより汎用的(母集団の正規分布を仮定しなくて良い)にしたもの

二乗誤差(MSE, RMSE)と絶対誤差(MAE)の使い分け

次の記事が考察として良さそうだった - MAE and RMSE — Which Metric is Better?

その中のこの表がうまく両者の差を表している

f:id:imslotter:20170517121558p:plain

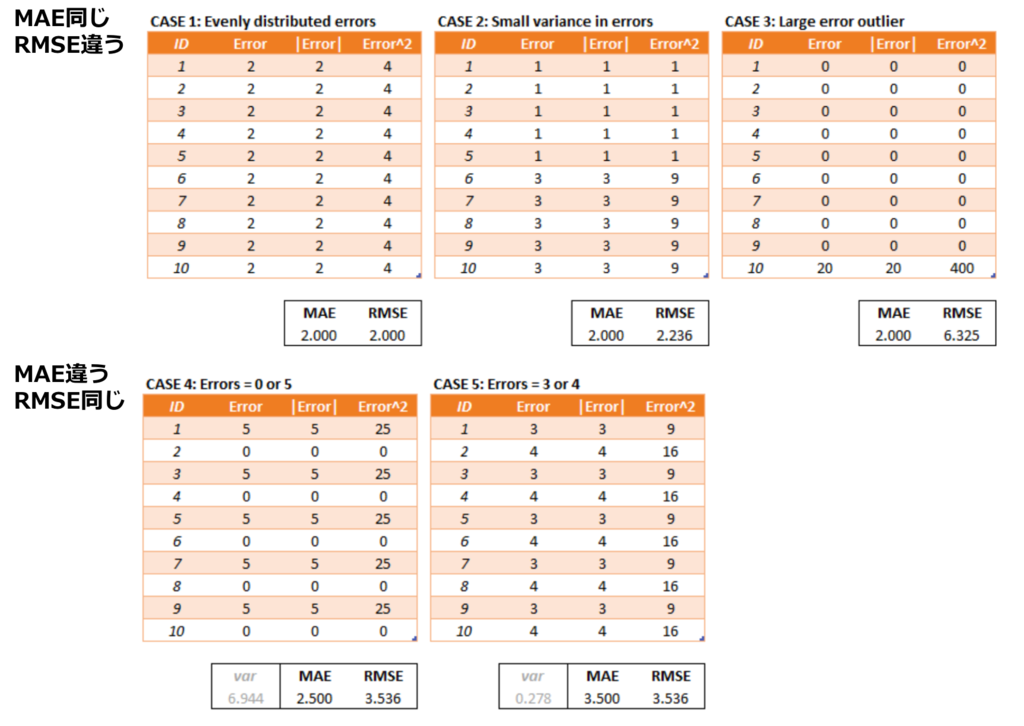
軽く結論をまとめておくと

RMSEは大きな誤差にペナルティを与えるのに適している
RMSEは局所的な誤差に左右されやすい。MAEの方が平均的
誤差としての解釈はMAEの方が明確にできる。RMSEはそれ自体が平均誤差を表している訳ではないので注意。

とのこと。

AICとBIC, wAICの使い分け

有意なパラメータが容易に識別できるような場合 : BIC
有意性が微妙なパラメータもモデルに含めたい場合 : AIC
真の分布(標本集団)を何も仮定することなく使う : wAIC

データ数が多いとBICの第二項が効いてくる。

時系列問題

HMMやRNNなど、時系列データを分析することもある。そういうときによく使われる指標。

用語	日本語	定義・意味
MSE RMSE MAE	*	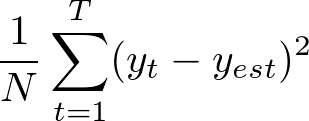など、回帰問題の誤差を時系列方法に展開すると使える。基本的な誤差
Dynamic Time Warping (DTW) Distance	動的時間伸縮法	2つの時系列の各点の距離を総当りで比較したときの、系列同士の最短距離。時系列の長さが違う場合でも適用可能*2
Perprexity	パープレキシティ	$\frac{1}{正解単語が選ばれる確率}$ 自然言語の分野でよく使われる(RNNの評価などでよく出てくる)参考記事
Regret	リグレット	最適値からどのくらい(確率論的に)外れるか。どっちかというとデータの評価というよりアルゴリズムの理論限界を示すのに用いられる。