こんにちは、ほけきよです
昨日は地震で目が覚めました。 久しぶりに揺れたので、怖かったです。
地震のときに起こる津波ですが、その危険さを表す写真が昔話題になってましたね

1mって、身長にも満たないんですよ? 「100%死ぬと言われても...実感わかない。」 と思っている方,多いのではないでしょうか
なので、今回は津波がどれほど危険なのか、ちょっと計算してみます! ちなみに、概算なので正確な値ではありません。予めご容赦を.
津波のヤバさ(絵)
 (気象庁より引用)
(気象庁より引用)
普通の高波とぜんぜん違うのは後ろに延々と続いた水の塊としてやってくるところです. 一旦押し流されたらもう終わりというのが視覚的にわかると思います。
水のヤバさ
普段何気なく存在する水ですが、かなり恐ろしい物質です。 密度は1[g/cm3]で、1mの立方体の中に水を敷き詰めると、なんと1トンにもなります。
1m立方って、人の身長より低いわけですから、それで1トンになるって、なんだか現実離れしていて怖いですよね。 でも、事実1トンなんです、小錦(250kg)4人分です*1。
カイジの沼パチンコ編を読んだことありますか? 彼らは、1m3の水を20個用意することで、ビルを傾けちゃいました。

(逆境無頼カイジ-破戒録篇-第19話『奇跡の軌道』より)
水はそのくらい重い物質なんです
- ポイント : 水の密度は 1[トン/m3]
津波の波長
さっきの図にも有りましたが、津波の波長はものすごく長いです。波長というのは、一つの波の長さのことです。
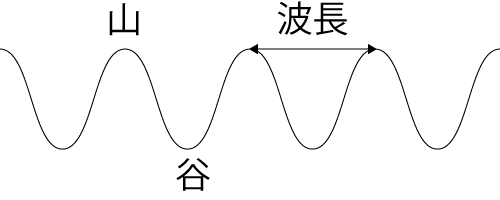
ものすごく長いということで、横からみると↓図のようになっていると考えられます。

ここでは波長を20kmとして計算すると波の1/4なので5kmの長さということになる。 横から見たときのこの領域の面積は、ほぼ三角形なので
1m×5000m×1/2 = 2500m2
となります。このくらいの水の量が押し寄せてくるということです。
- ポイント : 津波は波長がめちゃくちゃ長い。横から見た断面積は2500 m2くらいの水の量
人の表面積
さっきの量に人の前から見た面積(前方投影面積)をかけると、全体の水の量が分かります。
今回いろいろ調べたのですが、あんまり人の前方投影面積を書いてある文献が見つからなかったので、 画像分析で求めているyoutubeの動画を参考にします
これはこの技術でめっちゃ凄い。空気抵抗の計算とかが簡単にできそうですよね。
この人の身長が163cmなので、お辞儀をしているとちょうど1mくらいだろうということから ↓のときの投影面積を参考に、0.4m2としました
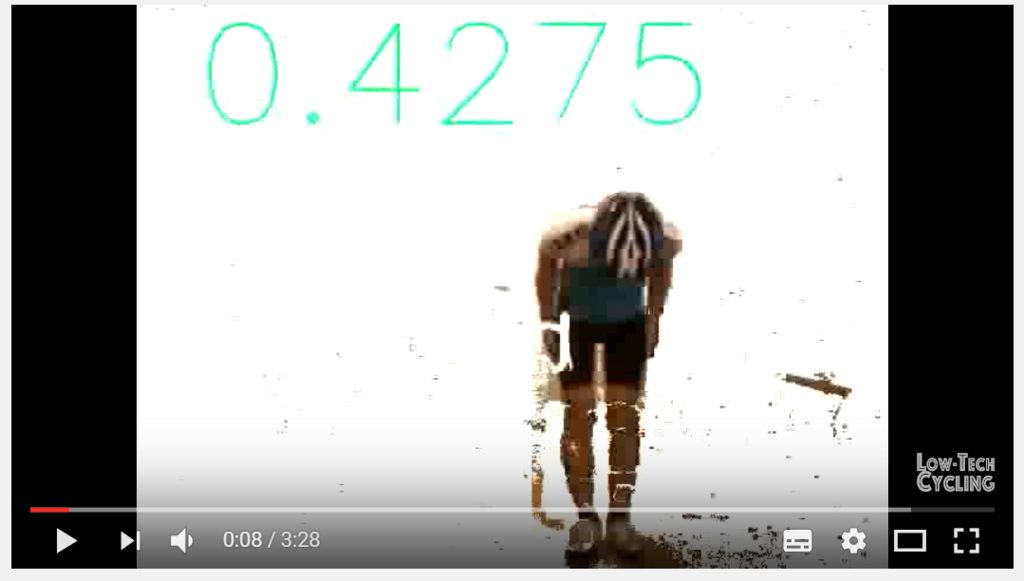
- ポイント : 人を正面から見たときの脚から1mのときの面積は大体0.4m2
人が一身に受ける水の重さ
人は脚から胴にかけては、大体長方形なので、面積から高さ1m、幅40cmの長方形の形だとします
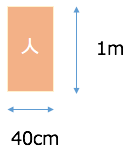
今回は概算なので、単純に
津波の断面積×人の横幅×水の密度
でかけ合わせると人が受ける水の重さが算出できます。

2500[m2]×0.4[m]×1 [t/m3] = 1000[t]
つまり、1000tの水を浴びるというわけです。ヤバイ
- ポイント:人が受ける水の重さは1000t
津波の速さ
浅水波理論というのがあって、津波の速さはだいたいで表されます。(gは重力加速度、hは水深)
到達したときの水深 = 波の高さだとすると
m/s
です。時速にすると約10km/hです。
- ポイント:1mの津波の速さはだいたい時速10km
1mの津波の持つエネルギー
時速10kmって、遅いと感じるかもしれません。でも、実際はものすごいエネルギーです
物理学では、エネルギー(E)は質量(m)と速度(v)で表されます
これを使うと、今回の波のエネルギーがどのくらいのエネルギーなのか、身近なもので表せます
何mの高さから落下?
エネルギー保存則
を使いましょう。ここでは60kgの男性&空気抵抗は無視とします
計算すると
[m]
7500mの高さからの落下と等価ですね。生き延びられますか??
10トントラックだと何キロに相当するの?
これもエネルギーを使って計算できます 10トンのトラックのスピードをvとすると
[m/s]
10トントラックだと時速100kmで衝突されるということと等価ですね。生き延びられますか??
まとめ
いかがでしょうか?? 概算なので突っ込みどころは多数あるかもしれませんが、危ないなと思ってくれたら幸いです!
ではではっ
