【ラグビー】日本と世界は実際どのくらいの実力差なの？レーティングから逆算してみた

f:id:imslotter:20191203220342p:plain

こんにちは、ほけきよです。

※スポーツアナリティクスAdventCalendar 5日目の記事になります。

「今年熱狂したスポーツを挙げてください。」

と言われると、まず間違いなく「ラグビー」が入ってくるのではないでしょうか。ONE TEAM!!!

日本開催のラグビーワールドカップ、大強豪アイルランド撃破、そして決勝トーナメント進出と、歴史的快挙に多くのファンが夢と感動をもらったことでしょう。

ワールドカップを終え、日本はなんと世界ランキング8位*1だそうです。ますます強くなる日本に、これからも期待ですね！

f:id:imslotter:20191203233147p:plain — 参考 WORLD RUGBY

世界ランキングはどうやって算出されているの？？
イロレーティングとは？
レートと実力の関係は？
イロレーティングとラグビーのレーティングの関係は？
実際の実力差はどのくらいなのか？
まとめ

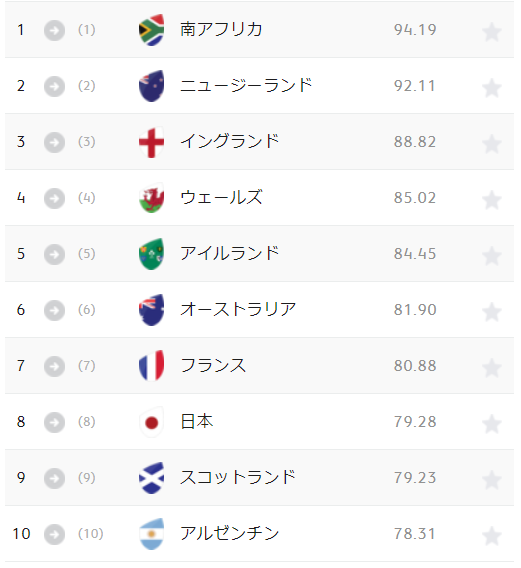
世界ランキングはどうやって算出されているの？？

ところで、このよく見かける「世界ランキング」、どのように付けられているのかご存知でしょうか？

ラグビーのランキングはポイントによる順序制で、簡単に言えば勝った人はポイントをGETし、負けた人はポイントを失う。そこに実力差の傾斜(弱いチームが強いチームに勝つとポイントが多くもらえる、等)がかかるというものです*2。この、実力差の傾斜をいい感じにポイント換算するというのがミソです。ラグビーでは、次のようなポイント配分になっています。

f:id:imslotter:20191204174449p:plain

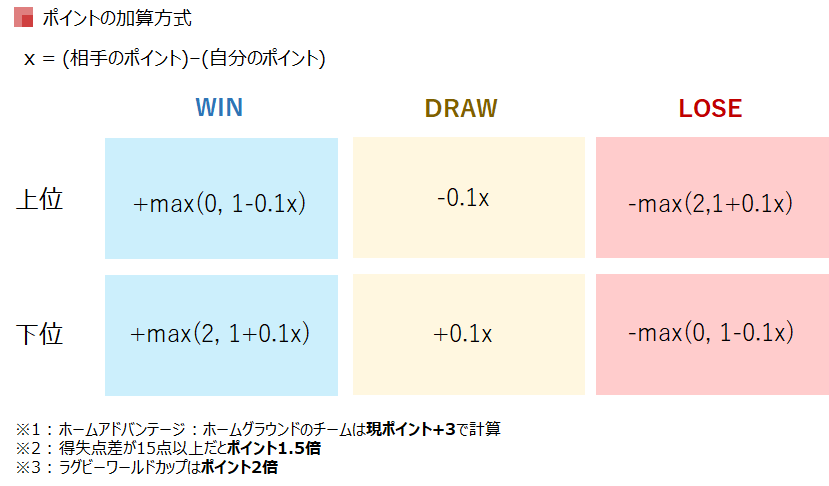
例えば、日本(80pt) VS 南アフリカ(95pt)で、日本が勝った場合、

$1+(95-80)\times0.1 = 2.5\mathrm{pt}$

が加算されます。逆に日本が負けた場合、

$1-(95-80)\times0.1 = -0.5\mathrm{pt}$

ですが、 $\max(-0.5,0) = 0$ なので、ポイントの変更はありません。

イロレーティングとは？

さて、対戦相手との実力の違いをうまくレーティングに反映する手法として、「イロレーティング」という手法が知られています。(ここでは大事なところだけ抜粋するので、実際の計算はWikipediaなどを参考にしてください。) *3

相対的な実力差を数値で表すときのスタンダードとなっていて、強さの違いがわかる**というのところがとても良い点です。ここでの強さの違いは、勝率の比です。例えばAがBの2倍強いというのは、Aの勝率67%、Bの勝率33%になる。ということです。

このレーティングは、2点の仮説の元成立しています。

イロレーティングの仮説

勝敗比は積で推移

勝ちか負けかの結果になる(基本的に引き分けはなし)

この２つ目は良いとして、1つ目がよくわからないですよね。簡単に言うと、「AがBの3倍つよくて、BがCの2倍つよかったら、AはCの6倍つよいよね」が成り立つということです。

f:id:imslotter:20191203231204p:plain

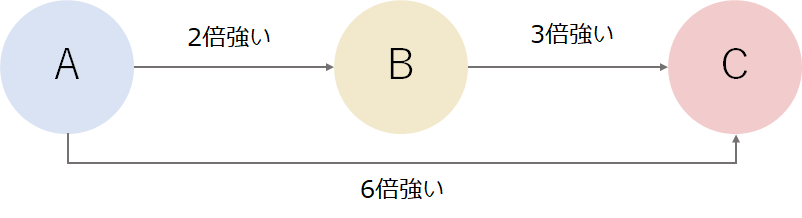
現実は相性などもあって上記の仮説の限りではないと思いますが、それでもある程度実力の反映されたレートになるので、多くのスポーツや対戦型ゲームなどで採用されています。事実、FIFAランキングはかなり純粋なイロレーティングを採用していて、*4例えば、レートが100高いと違うとおおよそ1.5倍強い。となるようにレートが設計されています。

レートと実力の関係は？

さて、何気なく言った、この「レートが100高いと違うと1.5倍強い」がイロレーティングの最も本質的な点です。「実力差の比率を点の差分で表現」している*5ことこそが、レートを見る上で大切な点なのです。つまり

× 100高いと1.5倍強い⇨200高いと $1.5\times2 = 3$ 倍強いではなく
〇 100高いと1.5倍強い⇨200高いと $1.5^{2} = 2.25$ 倍強い

となるわけです。レートの差は開くほど、その実力差は歴然としたものになります。

イロレーティングとラグビーのレーティングの関係は？

「ポイント差で実力の違いがわかる」イロレーティングが良いのはわかった。しかし、ラグビーのレーティングはイロレーティングにのっとってはいないので、そのままだと使えません。

「なんとかイロレーティングに換算できれば、実力差の近似値が出せるなぁ...」とぼんやり考えていました。

そう思いながら、両者「実力(レート)差と、配分されるポイント」のグラフを見比べてみたのです。その2つがこちら

f:id:imslotter:20191203232119p:plain

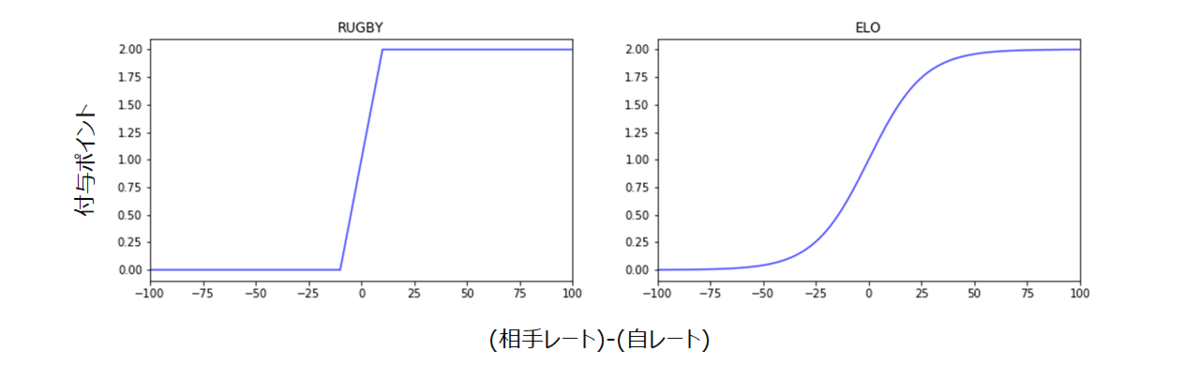
ふむ...なんだかとても似ていませんか？

「あれ？これイロレーティングの関数のパラメータを近似すれば、ラグビーのレーティングになるのでは？？」

と思ったので、関数を適当にフィッティングし、イロレーティングに使うパラメータを合わせてみることにしました*6。フィッティングしたグラフがこちら

f:id:imslotter:20191203232631p:plain

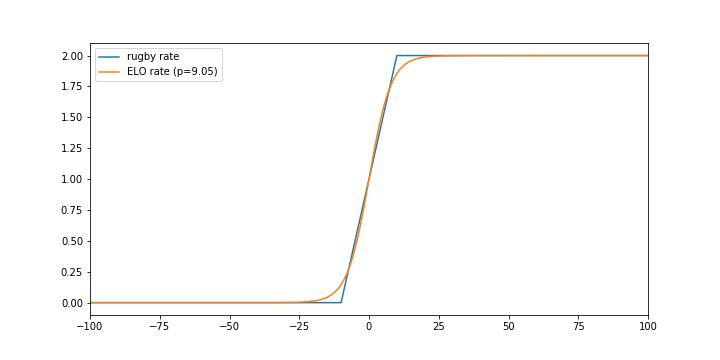
やはりカクついたところは表現しきれてはいませんが、ある程度うまく表せせている気がします。あとは、この近似式を用いて、レートから実力差への換算を行うだけです。これによって、レート差と実力差の変換近似式を手に入れることができました。それがこちら！

$W_{AB} = \frac{1}{10^{ (R_B-R_A)/9.05 }+1}$

$W_{AB}$ : AがBに勝つ確率
$R_{A}$ : Aのレート
$R_{B}$ : Bのレート

実際の実力差はどのくらいなのか？

さて、ここまで準備ができたら、あとは現行レートを代入するだけです。

日本と南アフリカ、アイルランドのレートを代入してみましょう。*7

$W_\mathrm{Japan wins SouthAfrica} = \frac{1}{10^{ (79.28-94.19)/9.05 }+1} = 0.0220$
$W_\mathrm{Japan wins Ireland} = \frac{1}{10^{ (79.28-84.45)/9.05 }+1} = 0.217$

日本が歴代最高順位の現レートで換算しても、勝率は2%なわけです。南アフリカに勝ったことが、アイルランドに勝ったことがどのくらい素晴らしい快挙かがわかると思います！さすが日本、ONE TEAM !!

まとめ

今回やったことを簡単にまとめておきます

今回やったこと

ラグビーのレートと実際の実力の関係を知りたいなぁ

イロレーティングというのは、レート差から実力差がわかる

ラグビーのレートをイロレーティングの式で近似する

近似した式にラグビーの実際のレートを代入する

日本と各国の実力差が知れた!うれしい!!ONETEAM!!!

という具合です。下式を使えば、実力値に換算できるので、皆さん積極的に使ってください！

$W_{AB} = \frac{1}{10^{ (R_B-R_A)/9.05 }+1}$

身近に使われている「FIFAランキング」や「ワールドランキング」などですが、こういう計算のもと行われているということ、知らない方も多かったのではないでしょうか。すこしでも頭の片隅にいれておくと、「このレート差の相手に勝つことはこんなにもすごいことなんだ！！」が数値を持って実感できるのではないでしょうか。ではではっ

今回の実装と計算結果はgithubにあげています。レーティングシミュレーターも作ってみました。なお、今回の計算は細かな部分(大会による点数配分の違い等)は省いています。計算や実装、論理のミスはあるかもしれませんので、こっそり優しく教えて下さい。

github.com

*1:2019/12/01現在

*2:実際には試合の重要度やホームでの試合か、などで傾斜の付き具合は違います。そのあたりはこちらが詳しいです

*3:参考イロレーティング(Wikipedia)

*4:2018年からレーティング方式が変わり採用されたようです

*5:つまり実力差の対数表示である

*6:あとから調べてみると、ラグビーのレーティングもイロレーティングをもとに作られているらしく、それはそうか。という感じでした。

*7:実際は、試合前のレートで語りたいのですが、試合前のレートを見つけることができなかったので、今のレートにしています。