【Day-21】統計的異常検知/変化検知の基本をまとめる

f:id:imslotter:20171221005033p:plain

世の中のデータ分析のニーズは、何らかの異常を発見したいというところに多くある。機械で言えば故障を検知する、マーケティングで言えば流行を発見する、株価で言えば相場変動を見つける...

普通と違うことを発見する技術、それが「異常検知/変化点検知」今回は下記二点の本を参考にしながら、異常検知とは何か？変化点検知とは何か？をぎゅっとまとめる

異常検知と変化検知

データマイニングによる異常検知では、確率モデルの違いに重きをおいて異常検知を分類している。

機能	入力対象	確率モデル	検出対象	応用
外れ値検知	多次元ベクトル	独立モデル (ガウス混合分布、ヒストグラム)	外れ値	不正検出故障検知
変化点検出	多次元時系列	時系列モデル ARモデル等	時系列の急激変化	攻撃検出障害予兆検出
異常行動検出	セッション時系列	行動モデル隠れマルコフモデル	異常行動パタン	なりすまし検出不審行動検出

異常検知と変化検知では、データの性質から異常検知を分類している。下図のように

f:id:imslotter:20171221040958p:plain

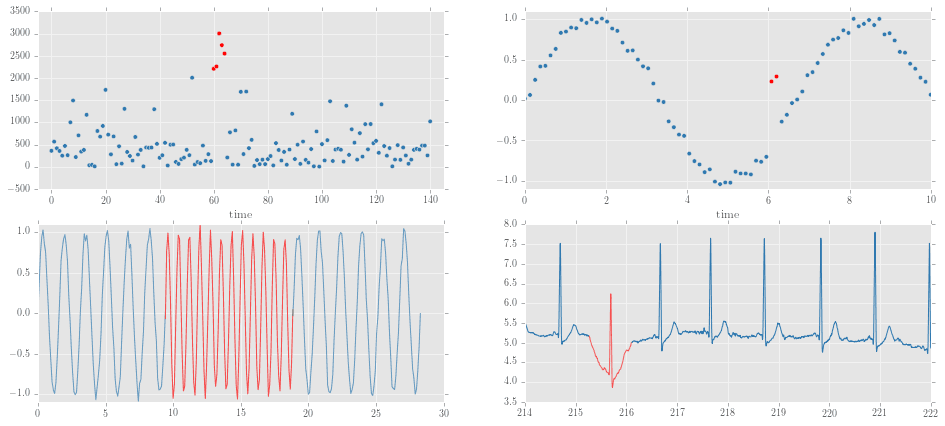
タスクによって、使うアルゴリズムも変わってくる。

統計的 = データが裏で、ある確率分布で動いていることを仮定

もうすこし噛み砕いて言うと、

学生時代を思い出してみる。みんなの平均点が30点なのに、一人だけ100点だったらヤバい。なぜヤバいのか。それを論理的に説明するために、 平均点周りで点数がイイ感じに散らばっているという仮定を置く。イイ感じの分布の一つが正規分布で、ソレを元に、定量的にどのくらいヤバいのかを計算していく。

さっきの例のヤバいを定量的に表すことができれば、どの程度異常なのかがはっきりと分かる。方法は、ラベル付きデータと、ラベルなしデータで違う。

ラベル付きデータの場合は、下図の様に正常・異常共に分布を描くことが出来るので、正常の確率分布と異常の確率分布の値の比から、新しく入力したデータを正常/異常を判定することが出来る。

これをネイマン・ピアソン決定則といい、次式で表す。

${\ln{\frac{p\left(x' | y=1,D\right)}{p\left(x' | y=0,D\right)}}}$ が所定のしきい値 ${\tau}$ を超えたら異常

この決定則は、正常な標本の精度を保ったまま、異常標本の精度を最大化するという条件付き最大化により数式で計算できる。計算方法に関してはコチラの記事が詳しい。

ひとことで言うと、ラベルデータの異常判定は正常/異常の対数尤度比から判定できるということ

多くのデータは正常が圧倒的に多くて、異常が少ない/無い。この場合、異常の分布が出せないので、全体のデータから判定する。 ありふれた観測値より「珍しい」観測値を得たほうが得られる情報量が大きいので、それを数式で表すと、対数尤度の負の対数になる。

値 $\mathbf{x'}$ に対する異常度 $a(\mathbf{x'})$ は
$a(\mathbf{x'}) = -\ln{p\left(\mathbf{x'}|D\right)}$ で表される。

基本的な異常の計算は上記のように、確率分布を仮定し、対数尤度を求めて計算する。

問題は確率分布 $p$ をどうするか。いつもデータがきれいな正規分布とは限らない。下記に、主要な分布と性質、計算方法をまとめる

分布	性質	計算方法
正規分布	単純な分布、大数の法則に従うようなデータには基本使えるので汎用性が高い	ホテリングのT²法(参考)
混合分布モデル	分布の山が２つ以上あるようなデータに適用できる。厳密計算が出来ない	EM法による近似計算(参考)
経験分布	分布を仮定せず、データから分布を作る。複雑な形を作れる一方で、データに左右されすぎて非直感的な結果になることも。	k近傍法/LoF (参考)
ガウス過程	入力と出力が同時に観測できる場合、ガウス過程により、関数を確率モデルで近似して異常検知に用いることが出来る	ガウス過程回帰(参考)
ミーゼス・フィッシャー分布	方向データ(長さ1で方向にだけ情報がある)に対する分布、自然言語などに対して用いられる	積率法(参考)