先日こんなツイートをしました。
数字ってのは、本来「誰が見ても同じ」と思われているから、インパクトと説得力がある。けど、実際そうはなっていないのが怖い。リテラシーのない人は簡単に間違って、心証を変えられる。高度な数学をできる必要は全くないけど、数字に踊らされない程度のリテラシーは身につけよう、書き手も読み手も。
— ほけきよ (@hokekiyoo) 2017年8月28日
読み手側は、意図された文章に対してだまされないように気をつけなければならないし 書き手側は、せっかく良い文章なのに「だまされた!!」などと思われるのも嫌でしょう。
そこで今回は事例とともに、「数字でヒトをだます方法と対処法」を紹介します。
年収1000万円は多い!?
数字よりも、可視化されたデータのほうが、先入観が入り込みやすいです。
たとえば↓のツイートで言及した例。
グラフリテラシーをつけようね。
— ほけきよ (@hokekiyoo) 2017年8月18日
例えばこれ。あたかも「1000万円以上の人が急に増えた!夢がある!」
とか思えるかもしれんけど、単に"目盛りの間隔が変わった"だけだよ。直感に反するところは「なぜ?」と考えようね😇 pic.twitter.com/Urh3GMZxhe
いきなりグラフ横軸の間隔が変わっているんです。
これでも、だまされるヒトはだまされて
「へえ、日本って1000万円以上稼いでいるヒトがたくさんいるんだ」
と思っちゃうでしょう。
グラフに騙されないようにしよう!
ほかにもグラフでヒトをだます方法はかなりたくさんあります。
詳しくはこの記事にまとめたので、ご覧になってください。
最もだましやすく、特に注意すべきポイントは
- グラフの縦軸、横軸は適切か
ここだけは、必ずチェックするようにしておきましょう。
日本の平均貯蓄が820万円?!
たとえば、
「日本人は平均貯蓄820万もある!!あなたはどうですか??」
という煽り文句があったとします。820万って、一般の人々特に若者が貯蓄できる額にしては多すぎるでしょう。
どうしてこんな非直感的な平均値になっているのでしょうか。
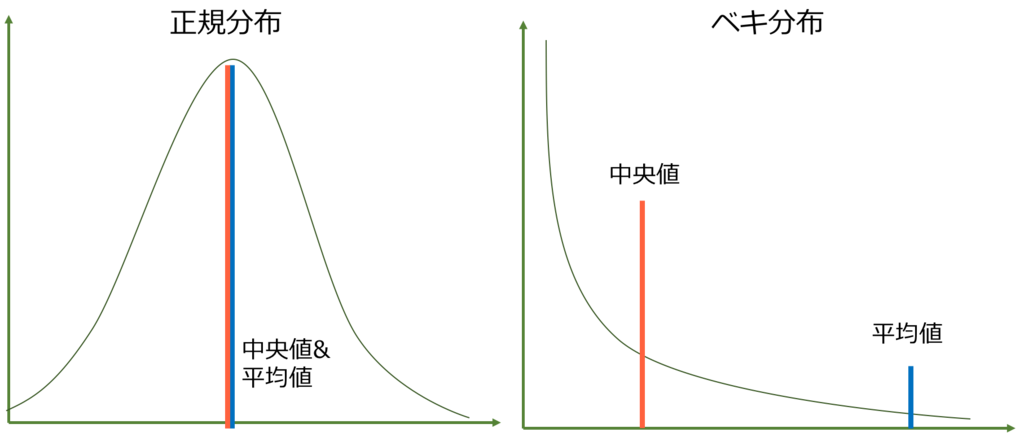
平均値と中央値
それは、貯蓄の分布が平均値にとって意味をあまりなさない分布になっているからです。
詳しくはこちらの記事に書いてあるのでどうぞ
皆さんは「二割八割の法則」を聞いたことがありますか?
世の中の2割の人が8割の利益を手にしているという法則です。
人間社会ではこのようなことが容易に起こります。
このようなときに平均は無意味です。一部の超絶金持ち集団に引っ張られるからです。
そういうときに大事なのが、中央値というわけです。
例えば1000人の貯蓄の中央値を求めたい時、溜まっている人を順番に並べ、500人目の値という具合です。
これが実は平均と違うのです。詳しくは↑の記事で!
グラフの形で判断すれば大きくは間違わないと思います。
くらいと思っておくと、大方外れないと思います。*1
「東大合格○○人!」
よくこんなチラシ、見ませんか?
「東大に入った中で1500人がこの塾を受けていました!」
これで、「よし、この塾にはいれば東大に入れる!」となります。
…
なりませんよね?なぜか?
実は、もっと大事な情報を隠しているからです。
論理は逆転していないか?
こういうのは図にするとわかりやすいので、図にしますね。
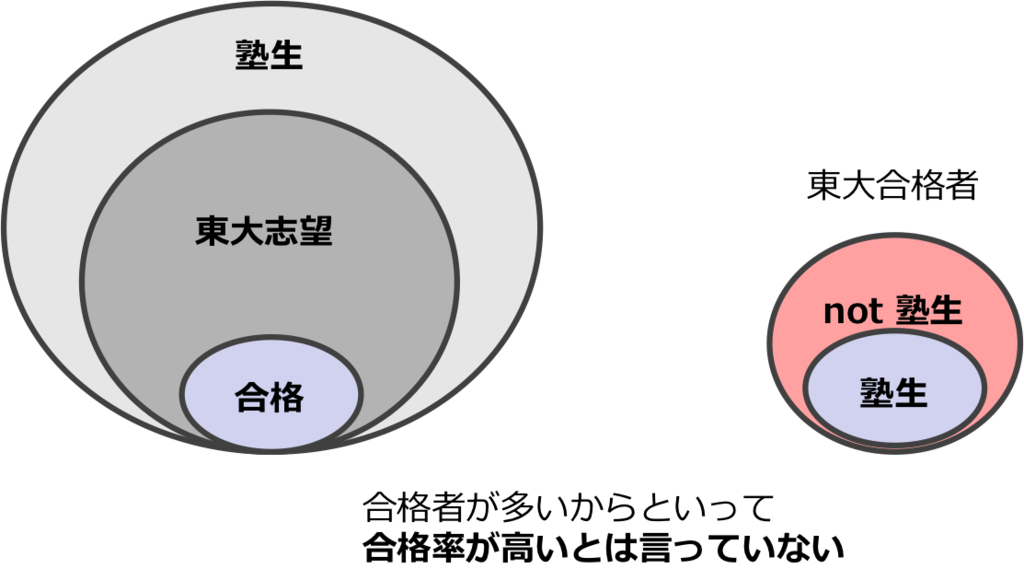
大事なのは、
- 東大志望のうち、何%が合格したのか
です。
「プロ野球選手は全員子供のころお米を食べていた」から、「お米を食べたらプロ野球選手になれる」とはなりませんよね。それと同じです。
論理の逆転が起こっていないか注意して見ておきましょう。
「小学生が一番TOEICができる」
こんな画像が出回っていました。
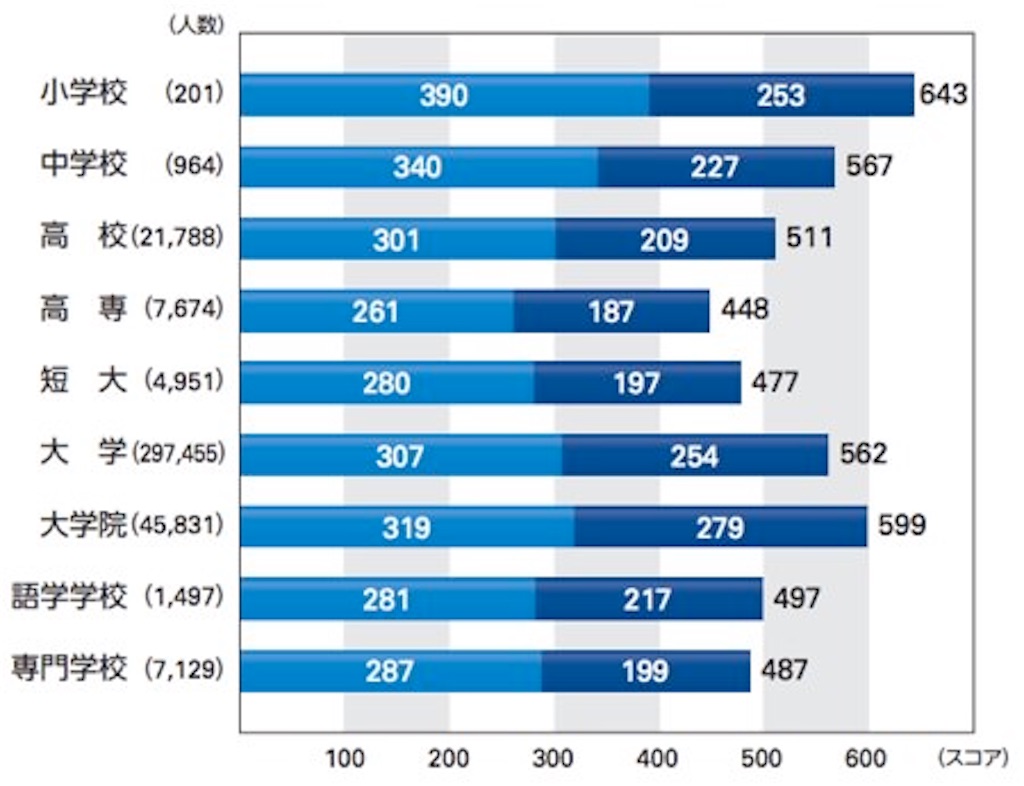
ふぅむ、嘆かわしい。世の大学生は小学生より英語ができないのか。 と思った方も多いと思います。
しかし、本当にそうなのでしょうか?
この手の統計結果は無作為に選ばれた母集団というのがとても大事です。
200人っていうのは、十分な数字だと思いますか?
この小学生200人は、無作為だと思いますか?
…
そんなわけありませんよね。むしろ、こう考えるのが正しいのです。
母集団を意識しよう
「小学生からTOEICを受けるような層は、英才教育を受けている英語に長けた人材で、大学生になるとほとんど強制で受けさされる。だから小学生のほうが平均点が高くなる」
図にするとこういうこと。
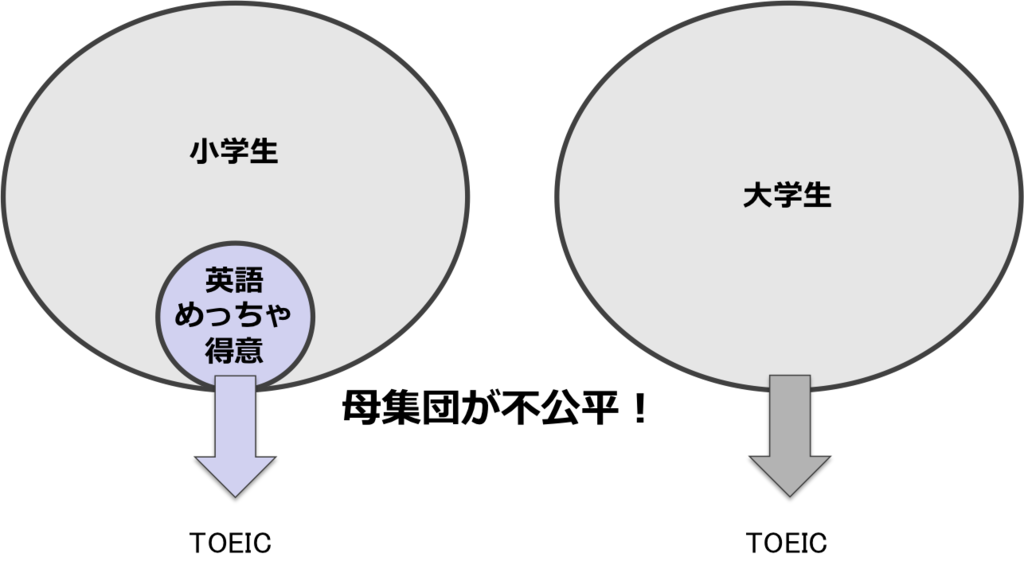
大事なのは母集団ですよ。いわゆる「生存バイアス」というのもこの母集団を誤って解釈した結果です。用意に騙せ騙されるので、つねに全体はどこにあるかを意識しましょう。
初任給が高い人は、お金持ちになれるよ!
たとえば、こんな文言があったとします。
「初任給が30万円以上のヒトは全体の5%、30歳になって、年収が1000万円以上のヒトは全体の5%。つまり、初任給が30万円以上のヒトの多くは30歳で年収が1000万円に到達する!!!」
一見「ふぅむ、なるほど。」となりそうですが、本当にそうですか?
相関と因果
実はこの文章、論理が通っていません。どこが間違っているのでしょうか。
- 30万円以上のヒトと、年収1000万円のヒトはこの文章の限りではまったくの無関係である
ことが一番の間違いなのです。
こういう時に見ないといけないのが、2つの相関です。
大事なのは、2つの独立した事実ではなくて初任給30万円以上だった人が、30歳で1000万になっているかどうかなのです。
初任給30万円の人と、30歳で年収1000万の人が違うと、全くの無意味なのです。
まとめ
いかがでしたか?
このように、簡単に数字で人を騙すことができますし、騙される人も多いでしょう。 この手の話はいくらでも思いつきますし、もっと高度な数学を使えば、ますます相手を混沌と誘うこともできます。
でも、個人的には科学は人々を幸せにするために使いたいものです。
皆さんがリテラシーを持つことで、不幸せになる人がすこしでも減るといいなって、思います。ではではっ!
*1:本当は、もっと分布はいろいろあるので、それぞれの性質を知っておいたほうが好ましいのですが、まあ代表的な2つの形でOKでしょう。